10667. Intervals on tree
We have a tree with n vertices and n 1 edges, respectively numbered 1, 2, ..., n and 1, 2, ..., n − 1. Edge i connects vertices ui and vi.
For integers L, R (1 ≤ L ≤ R ≤ n),
let us define a function f(L, R) as follows:
·
Let S be the set of the vertices
numbered L through R. f(L, R) represents the number of
connected components in the subgraph formed only from the vertex set S and the
edges whose endpoints both belong to S.
Compute
![]()
Input. The first line contains
number n (1 ≤ n ≤ 2 * 105). Each of the next n 1 lines contains two
vertices (ui, vi) (1 ≤ ui, vi ≤ n) an edge in the graph.
Output. Print the value of the sum.
|
Sample input |
Sample output |
|
3 1 3 2 3 |
7 |
SOLUTION
graphs depth
first search
Algorithm analysis
Let V be the set of
vertices in the tree, E be the set of edges. Then the following formula holds
for a tree:
|V| = |E| +
number of connected components
Then the number of
connected components f (L, R) can be calculated as |V| |E|, where
·
V = nodes(L, R) set of
vertices {L,
, R};
·
Ε = edges(L, R) set of edges with endpoints in {L,
, R};
The required sum
res = ![]() can be
computed using the following algorithm:
can be
computed using the following algorithm:
res = 0;
for
(L = 1; L ≤ n; L++)
for
(R = L; R ≤ n; R ++)
res
+= nodes(L, R) edges(L, R)
Let S(n)
= 1 + 2 +
+ n.
Let L = 1. Then as R we can
choose the vertices 1, 2,
, n.
![]() = nodes(1, 1) + nodes(1, 2) +
+ nodes(1, n) =
= nodes(1, 1) + nodes(1, 2) +
+ nodes(1, n) =
1 + 2 +
+ n
= S(n)
Let L = 2. Then as R we can choose the vertices 2,
, n.
![]() = nodes(2, 2) + nodes(2, 3) +
+ nodes(2, n) =
= nodes(2, 2) + nodes(2, 3) +
+ nodes(2, n) =
1 + 2 +
+ n
1 = S(n 1)
Let L = k. Then as R we can choose
the vertices k,
, n.
![]() = nodes(k, k) + nodes(k, k + 1) +
+ nodes(k, n)
=
= nodes(k, k) + nodes(k, k + 1) +
+ nodes(k, n)
=
1 + 2 +
+ n
k + 1 = S(n k + 1)
Thus
![]() = S(n) + S(n 1) +
+ S(1)
= S(n) + S(n 1) +
+ S(1)
This sum equals to the sum of all numbers in the
following table:
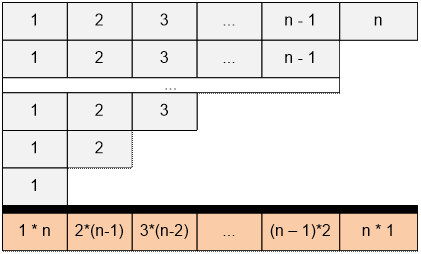
The table contains n ones, (n 1) twos, (n 2) triples, and so on.
The sum can be rewritten as
![]() = 1 * n
+ 2 * (n 1) + 3 * (n 2) +
+ (n 1) * 2 + n * 1
= 1 * n
+ 2 * (n 1) + 3 * (n 2) +
+ (n 1) * 2 + n * 1
It is known that
·
![]() =
= ![]() ,
,
·
![]() =
= ![]()
Then
![]() =
= ![]() =
=![]()
![]() =
=
![]()
![]() =
= ![]() =
= ![]()
Consider an edge of a tree (u, v). It will be included in
all sets of edges (L, R), where L ≤ u and v ≤ R.
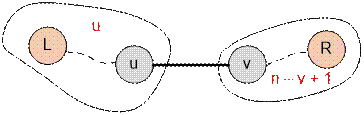
The value of L can be chosen in u ways, and the value
of R can be chosen in (n
v + 1) ways. Therefore, the number of
sets edges(L, R) which the edge (u, v) belongs to is u * (n
v + 1).
Example
We have six possible pairs
(L, R) as follows:
·
For L = 1, R = 1, S = {1} and we
have 1 connected component.
·
For L = 1, R = 2, S =
{1, 2} and we have 2 connected components.
·
For L = 1, R = 3, S =
{1, 2, 3} and we have 1 connected component,
since S contains both endpoints of each of the edges 1, 2.
·
For L = 2, R = 2, S = {2} and
we have 1 connected component.
·
For L = 2, R = 3, S =
{2, 3} and we have 1 connected component,
since S contains both endpoints of Edge 2.
·
For L = 3, R = 3, S = {3} and
we have 1 connected component.
The sum of these values is 7.
Find the answer using a formula:
![]() =
= ![]() =
= ![]() = 10
= 10
·
edges(1, 3) = 1;
·
edges(2, 3) = 2 * 1 = 2;
Therefore the answer is 10 1
2 = 7.
Algorithm realization
Read the value of n.
scanf("%d", &n);
Initialize res with value ![]() =
= ![]() .
.
res = 1LL * n * (n + 1) * (n + 2)
/ 6;
Iterate over
the edges (u, v). Set u ≤ v. For each edge, subtract the value u * (n
v + 1) from the sum.
for (i = 0;
i < n - 1;i++)
{
scanf("%d %d", &u, &v);
if (u > v)
{
temp = u; u = v; v = temp;
}
res -= 1LL * u * (n - v + 1);
}
Print the
answer.
printf("%lld\n", res);